Будинок Блог~~Детальний посібник з повного додавання~~

~~на 2024/05/10~~ ~~598~~

Детальний посібник з повного додавання

У царині цифрової електроніки та комп'ютерної інженерії додатки представляють один з найважливіших будівельних блоків, ключові у побудові та функціональності більш складних арифметичних ланцюгів.Як інтегральні компоненти арифметичної логічної одиниці (ALU), добавки полегшують численні обчислювальні операції, починаючи від основних арифметичних до складних логічних завдань, необхідних для системних операцій.Їх дизайн, який може змінюватись від простих напівдоказів до більш складних повних добавок, відіграє вирішальну роль у підвищенні ефективності та швидкості обробки в цифрових системах.Ця стаття заглиблюється в детальну архітектуру та функціональні нюанси різних типів добавок, що ілюструє їх критичну роль у сучасній обчислювальній технології та досліджуючи їх експлуатаційну логіку, схему та додатки в більш широкому контексті цифрової логіки.

Каталог

1. Що таке прихильність?

2. Половина додавання

3. Повна додавання

4. Таблиця правди повної Аддера

5. Характеристики рівняння повного додавання

6. Реалізація повної схеми додавання

7. Переваги та недоліки повних доповнень

8. Застосування повних доповнень у цифровій логіці

9. Приклади повного реалізації

10. Висновок

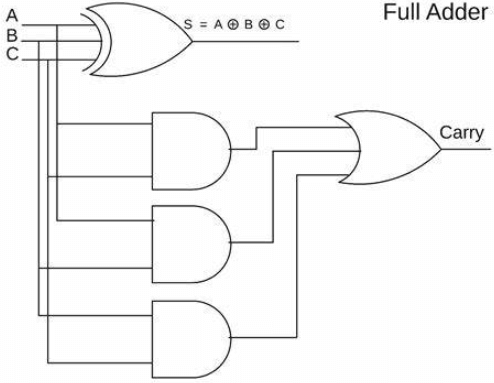
Рисунок 1: Повний приладдя

Що таке прихильність?

Аддер - це фундаментальний компонент в електронному інженерному та цифровому логічному дизайні та відіграє центральну роль у складніших комп'ютерних системах.У рамках арифметичної логічної одиниці (ALU) Аддер обробляє різноманітні важливі обчислювальні завдання.Ефективність та продуктивність всього процесора безпосередньо впливають на конструкцію та функціональність додавання.

У процесорі Аддер використовується не лише для основних арифметичних операцій, таких як додавання та віднімання, але й бере участь у більш широкому діапазоні логічних операцій.Наприклад, під час запуску програм процесору часто потрібно обчислити нові адреси пам'яті.Зазвичай це робиться шляхом додавання або віднімання з поточної адреси - завдання, яке виконується додавцем.Вони контролюють кількість ітерацій петлі та загальний потік шляхом збільшення та зменшення лічильників.У більш складних додатках, таких як індексація таблиці, доповнення швидко знаходять дані, обчислюючи зміщення.Це важливо для систем управління базами даних, побудови компілятора та масштабної обробки даних.Додатки також є ключовими для впровадження певних методик відображення в багаторівневих системах кешу, використовуючи арифметичні операції для визначення положення даних у кеші, тим самим оптимізуючи ефективність доступу.

Технологічно доповнення реалізуються за допомогою різних конструкцій схеми, включаючи паралельні, серійні та трубопровідні доповнення.Паралельні доповнення віддають перевагу своїй здатності одночасно обробляти декілька цифр, що робить їх придатними для сценаріїв, що потребують швидких обчислень.Серійні добавки, з іншого боку, обробляють один біт на годинник і ідеально підходять для обмежених ресурсами або низькою потужністю.ПОДАТКОВІ ПОДАКИ ДІЙДИ ПРОЦЕСУ ДОПОМОГУ на кілька етапів, кожна з яких обробляє частину операції додавання.Ця конструкція значно підвищує швидкість обчислень, особливо у високоефективних обчислювальних умовах.

Наполовину

Схема з напівпідробдям-це фундаментальний будівельний блок цифрової електроніки, спеціально розроблений для додавання двох одиночних двійкових цифр.Ця схема утворює основу повного додавання і є ключовим для розуміння більш складних конструкцій логічних схем.У половині додавання є два первинні входи, позначені A і B, які представляють Augend та додавання відповідно.Ця установка дозволяє йому обчислити суму та переносити вихід без необхідності введення перенесення з попередніх розрахунків.

Ядро напівдостороби складається з двох логічних воріт: воріт Xor та An і ворота.Ворота XOR відповідають за генерування виводу суми.Він працює за простим правилом, де він виводить 1, якщо лише один з його входів - 1;В іншому випадку він виводить 0. З іншого боку, і ворота обробляє вихід перенесення.Він виробляє 1 лише тоді, коли обидва його входи дорівнюють 1, ідеально узгоджуючись з основними вимогами бінарного додавання.

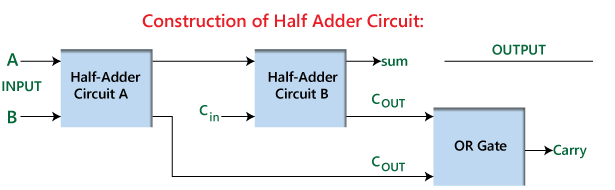
Малюнок 2: Будівництво половини

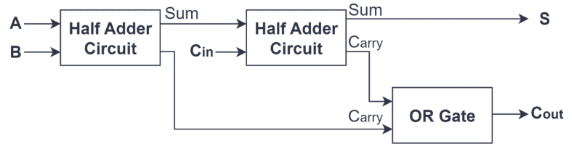
Ця ефективна та проста конструкція дозволяє половині додавця не тільки виконувати базове бінарне додавання незалежно, але й служити будівельним блоком для створення повного додавання.Повний додавець побудований шляхом поєднання двох напівдиводів з додатковими або воротами.У цій установці перша половина Adder приймає первинне завдання додавання, генеруючи попередню суму та перенести.Потім другий тайм Adder обробляє перенесення з першого разом із додатковим входом перенесення.Нарешті, ворота або ворота об'єднують два виходи, що переносять, для отримання кінцевого виводу перенесення.Ця композиція підвищує функціональність додавання, що дозволяє йому виконувати більш складні багато-бітові завдання додавання, демонструючи широко розповсюджене застосування та важливість половини доповнень у дизайні цифрових ланцюгів.

Повна додавання

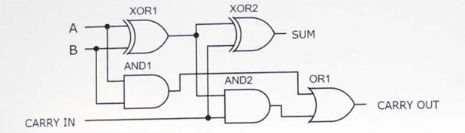
Повний додавець-це вдосконалений компонент цифрової логічної конструкції, оснащений для додавання трьох одноразових бінарних входів, які зазвичай позначаються як A, B та перенос (CIN).Ця конструкція дозволяє повному додавці ефективно обробляти складні бінарні доповнення, включаючи перенесення з попередніх обчислень нижчого порядку в одну операцію.

Малюнок 3: Повна схема додавання

Функціонально повний додавець може виводити двозначну суму, що означає, що його вихід може становити від 0 до 3, а також може виробляти проведення (COUT).Це трапляється томуДодаткову перенесення потрібно передати наступному вищому біт.

Структурно, повна додавання, як правило, складається з двох напівдидатів та однієї або воріт.Аддер першої половини приймає входи A і B, генеруючи початкову суму та сигнал перенесення.Потім цю початкову суму годують разом із перенесенням (CIN) у другу половину.Роль другого тайму Аддера полягає в тому, щоб додати цю суму з першого тайму до CIN, створюючи ще одну суму та новий вихід.Одночасно виведення перенесення з першого тайму додавання та виводу перенесення з другого тайму об'єднуються через або ворота, що завершується остаточним проведенням (кут) повного додавання.Конструкція цієї структури гарантує, що повна адміністрація ефективно обробляє розповсюдження перевізників, а також операції, що робить його ідеальним для виконання мульти-бітних бінарних доповнень.Таким чином, конструкція повного додавання не тільки прискорює обробку даних та підвищує ефективність, але й спрощує складність реалізації обладнання за допомогою прямої комбінації логічних воріт, що робить його незамінним компонентом у багатозначному додаванні та арифметичній логічній одиниці (ALU.).

Параметри	Наполовину	Повна додавання
Опис	Половина Adder - це комбінаційна логіка Схема, яка додає дві 1-бітові цифри.Напівпідробник виробляє суму з двох входи.	Повна додавання - це комбінаційна логіка схема, яка виконує операцію доповнення на трьох однопідрозділених двійкових числах. Повний прилад дає суму з трьох входів та значення перенесення.
Попереднє перенесення	Попередній перенос не використовується.	Попередній перенос використовується.
Вхід	У половині додавання є два вхідні біти (a, Б).	У повному обсязі є три вхідні біти (A, b, c_у.).
Виходи	Генерований вихід-два біт-суми і переносити з входу 2 біт.	Генерований вихід-два біт-суми і переносити з входу 3 біт.
Використовується як	Ланцюг напівдостороби не може бути використаний у так само, як і схема повного адвоката.	На місці можна використовувати повну схему додавання з половину ланцюга.
Означати	Це просто і прості в реалізації	Дизайн повного додавання не такий Простий як половина.
Логічний вираз	Логічний вираз для половини приладдя: S = a⊕b;C = a*b.	Логічний вираз для повного додавання є: S = a⊕b⊕cin;C_поза= (ab)+(c_у(a⊕b)).
Логічні ворота	Він складається з однієї колишньої воріт і однієї та ворота.	Він складається з двох колишніх, двох і воріт, і одна або ворота.
Заявки	Він використовується в калькуляторах, комп’ютерах, Цифрові вимірювальні пристрої тощо.	Він використовується в декількох додаваннях, Цифрові процесори тощо
Альтернативна назва	Немає альтернативної назви на половину Аддер.	Повний прилад також відомий як пульсація Аддер.

Графік 1: Різниця між половиною додавання та повним пристосуванням

Повна таблиця правдивості

Таблиця істини повного додавання є ключовим фактором для розуміння його оперативної логіки, що деталізує точну взаємозв'язок між бінарними вхідними комбінаціями та їх відповідними результатами.Ця таблиця демонструє всі потенційні сценарії введення та їх результати, що робить його важливим інструментом у розробці та перевірці цифрових логічних схем.Повний Adder обробляє три входи: A, B та A Ant (CIN), кожен з яких може бути або 0, або 1. Це призводить до восьми можливих комбінацій входів.

Для кожної з цих комбінацій результати з повного додавання включають суму (сумум) та проведення (cout).Сума-це додавання модуля-2 (операція XOR) трьох входів-A, B та CIN.Виконання відбувається, коли щонайменше два вхідні біти-1. Це відображає повну здатність додавання впоратися з перенесенням у послідовних операціях додавання, забезпечуючи точність у вищих розрахунках.

Щоб проілюструвати, розглянемо сценарій введення, де всі входи становлять 0 (a = 0, b = 0, c-in = 0).Сума виходу буде 0, а перенос також буде 0, що вказує на те, що немає додаткової суми або перенесення для управління.Якщо лише один вхідний біт становить 1, наприклад A = 1, b = 0, c-in = 0, сума виходу буде 1 без перевезення, що показує, що немає необхідності переносити перенос на більший біт.Коли два вхідні біти 1, як-от A = 1, b = 1, c-in = 0, сума виходу становить 0 (оскільки 1+1 дорівнює 2 у двійкових, а модулі-2 призводить до 0), але перенесення-Виходить 1, що вказує на перенесення, яке потрібно передати до наступного вищого біт.Найскладніший сценарій виникає, коли всі три вхідні біти-1 (a = 1, b = 1, c-in = 1);Сума виходу становить 1, а є проведення 1, що дозволяє припустити, що управління перенесенням також може знадобитися при ще більш високих бітах.

	Б	C_у	S	C_поза
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Діаграма 2: Повна таблиця правдивості

Характеристики рівняння повного додавання

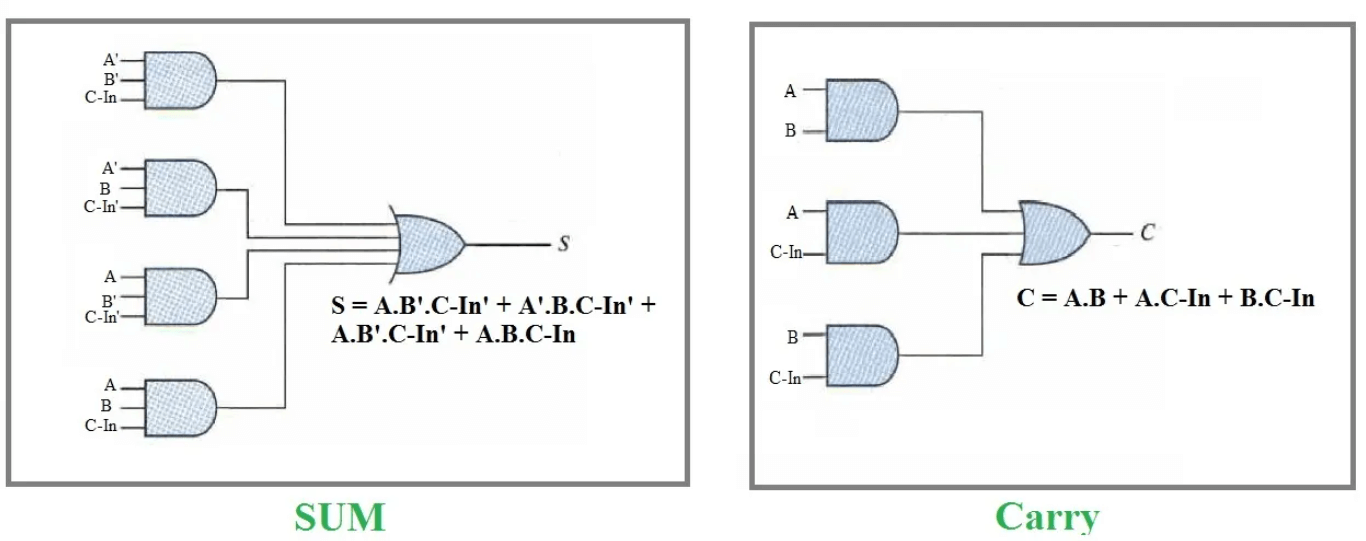
Розуміння повного додавання передбачає розсічення своєї функціональності за допомогою таблиці істини, де різні комбінації вхідних значень A, B та C-In призводять до випусків суми та кут.Щоб зрозуміти операцію, ми спрощуємо логічні рівняння поетапно.

Логічний вираз суми

Рівняння починається з різних випадків, коли сума дорівнює 1:

• A 'B' CIN + A 'B CIN' + A B 'CIN' + AB CIN

Це рівняння може бути ущільнене шляхом групування термінів з CIN та без нього:

• cin (a 'b' + ab) + cin '(a' b + a b ')

Це спрощення призводить до більш легкої для реалізації форми:

• Cin XOR (A XOR B)

Це представлення показує, що вихід суми по суті є операцією XOR серед A, B та CIN, фіксуючи основну поведінку бінарного додавання, де сума перемикається на основі непарної кількості.

Логіка для COUT

Починаючи з умов, де створюється перенесення:

• A 'B CIN + A B' CIN + AB C-In ' + AB CIN

Спрощуючи рівняння, ми визначаємо терміни, які зазвичай передбачають генерування перенесення:

• AB + B CIN + A CIN

Шукаючи ще один метод реалізації COUT, рівняння можна переорганізувати:

• AB + A CIN + B C-In (A + A ')

Це розширюється та рекомбіни, щоб зафіксувати всі сценарії, де принаймні два входи - 1:

• ab cin + ab + a c-in + a 'b cin

• AB (1 + CIN) + A C-In + A 'B CIN

• AB + A C-In (B + B ') + A' B CIN

• AB + A B 'CIN + A' B CIN

• AB + CIN (A 'B + A B')

Кінцева компактна форма для COUT:

• AB + CIN (A XOR B)

Ця версія рівняння виконання демонструє, як виробляється COUT або коли A, і B-1, або коли один із A або B становить 1 разом із перенесенням, тим самим інкапсулюючи логіку, необхідну для управління поширенням у багато-Біт двійкового додавання.Ця впорядкована логіка особливо корисна для впровадження ефективних цифрових схем.

Малюнок 4: Рівняння повного додавання

Впровадження повної схеми додавання

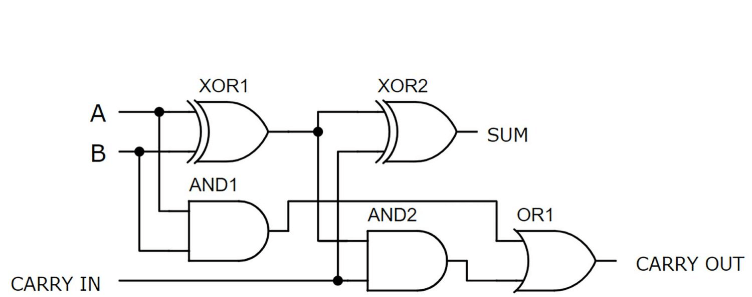
Впровадження повної схеми додавання передбачає ретельно збирання двох напівдимейців та воріт або ворота, щоб створити пристрій, здатний ефективно обробляти додавання трьох одноразових бінарних входів.Таке розташування оптимізує складність схеми та забезпечує як ефективні, так і точні обчислення.

Для початку, перша половина Adder займає два первинні бінарні входи, A і B, які є основними цифрами, які слід додати.Ключовим завданням є обчислення суми та початкового перенесення цих двох чисел.Тут, перша половина Adder забезпечує два результати: початкова сума (SUM1) та початковий перенос (перенесення1).SUM1 походить від операції XOR A і B, що вказує на те, чи є загальна кількість непарного числа 1.Перенос1, результат операції та експлуатації між A і B, вказує на те, чи є обидві цифри 1, що вимагає перенесення до наступного вищого біт.

Далі, другий тайм приєднується до процесу.Він використовує сумум SUM SUM1 та третій вхідне CIN (переносять з попереднього розрахунку) як його входи.Друга половина виробляє два результати: остаточний результат (SUM2) та вторинний перенос (перенос2).SUM2, який є результатом XOR SUM1 та CIN, являє собою остаточну суму трьох входів, що відображає агреговане бінарне додавання.Перенесення2, що виникає з операції та операції між SUM1 та CIN, вказує на перенесення, що утворюється цими компонентами.

Full Adder Circuit with Using Two Half Adder

Малюнок 5: Повна схема додавання з використанням двох половини додавання

Нарешті, для завершення повного дизайну доштувача або ворота необхідні для обробки виводів перенесення 1 і перенесення2 від обох половин.Цей або ворота гарантує, що будь -який перенос, що утворюється під час обчислень, буде правильно переадресовано на кінцевий вихід.Тому остаточний вихідний вихід Adder (COUT) є або результатом перенесення1 та перенесення2.Включення цього або ворота гарантує, що всі потенційні носи точно обчислюються та передаються на наступний рівень в багатокутних операціях додавання, забезпечуючи цілісність арифметичної операції на декількох бітах.

Переваги та виклики повних добавок у цифровій логіці

Повні доповнення відіграють незамінну роль у цифровому дизайні логіки, пропонуючи численні переваги, які роблять їх важливими для різних сценаріїв обчислювальної та обробки даних.Їх основні переваги включають неабияку гнучкість, швидкі швидкості обробки та ефективне управління перенесенням.Ці риси роблять повні добавки ідеальними для виконання складних арифметичних операцій та логічних функцій, особливо в додатках, що потребують послідовного багаторозділення.

Переваги

Гнучкість: Повні добавки переважають у своїй здатності одночасно обробляти кілька бінарних входів (A, B та CIN).Їх також можна розширити на більші масиви дошки для обробки довших двійкових чисел.Ця масштабованість важлива для побудови високоефективних арифметичних логічних одиниць (ALUS), які повинні виконувати складні багатопідрозділені арифметичні та логічні операції.

Швидкість: Завдяки їх внутрішній архітектурі паралельної обробки, повні доповнення можуть завершити додавання всіх входів за один тактовий цикл, а також визначити виведення.Ця здатність підтримує безперервні операції з додавання та є незамінною для обробки даних у режимі реального часу в сучасних мікропроцесорах та високошвидкісних обчислювальних пристроях.

Недоліки

Однак повні добавки також представляють помітні недоліки:

Складність у дизайні та впровадженні: Повні доповнення включають кілька логічних воріт та багаторівневі перенесення розповсюдження, що робить їх дизайн складним.Ця складність не тільки збільшує виробничі витрати, але також може вплинути на надійність ланцюгів.

Проблеми з затримкою поширення: Проведення розповсюдження може пройти через кілька логічних воріт, кожен з яких додає його затримку.Це може обмежити загальну обчислювальну швидкість під час масштабних операцій, особливо в обширних комп'ютерних системах та в розробці дуже великої інтеграції (VLSI) та високошвидкісних процесорів.Затримка може стати значним вузьким місцем у продуктивності.

Щоб пом'якшити ці проблеми, інженери постійно досліджують більш ефективні конструкції схеми.Стратегії включають використання більш швидких технологій логічних затворів, оптимізацію макетів схеми для скорочення довжини шляху та розробки передових технологій, таких як доповнення, щоб мінімізувати затримки в перенесенні поширення.

Програми повних доповнень у цифровій логіці

Повні доповнення широко використовуються в цифровій логіці, цінуються за їх гнучкість та ефективність, що робить їх центральними для безлічі завдань обчислень та обробки даних.Їх застосування охоплює основні арифметичні операції до складної обробки сигналів та контролю системи.Ось детальний погляд на деякі ключові сфери, де повні доповнення є невід'ємними.

Арифметичні схеми

Одне з найбільш простих використання повних добавок - це арифметичні схеми, де вони виконують двійкове додавання.Особливо важливим для додавання до кількості кількості, повні доповнення керують довшими бінарними послідовностями за допомогою каскадування.У цій композиції кожен повний додавець обробляє доповнення до свого бітового положення та перенесення з нижнього біт, а потім передає новий перенесення до повного додавання наступного вищого біт.Цей каскад дозволяє комплексне багаторозділення додавання у всьому діапазоні цифр.

Обробка даних

Повні добавки також відіграють ключову роль у вдосконалених завданнях з обробки даних, таких як цифрова обробка сигналів (DSP) для фільтрації та перетворення Фур'є, де потрібні точні та швидкі арифметичні операції.Крім того, у царині інформаційної безпеки, включаючи шифрування даних та алгоритми виявлення помилок та виправлення, такі як перевірка паритету та генерація коду циклічної надмірності (CRC), повні додатки мають вирішальне значення для виконання основних операцій BIT.

Лічильники

У цифрових лічильниках повні добавки є незамінними для реалізації функцій збільшення та зменшення, особливо в модульних та синхронних лічильниках.Вони точно керують носіями та запозиченнями, щоб забезпечити точний підрахунок.

Мультиплекси (MUX) та демульплексатори (Demux)

У мультиплексах та демульплексах повні добавки відіграють вирішальну роль у виборі каналів та розподілі даних.Вони беруть участь у логіці, яка визначає, які канали використовуються для введення та виведення даних, що приймають рішення на основі логічних сигналів управління.

Технологія пам'яті

У адресі пам'яті повні доповнення допомагають генерувати адресні сигнали для динамічного доступу до місця пам'яті.Це особливо важливо в динамічній пам’яті з випадковим доступом (DRAM) та інших системах зберігання, де повні доповнення підтримують складні розрахунки адрес для підвищення ефективності доступу до пам'яті.

Арифметичні логічні одиниці (ALU)

Нарешті, як фундаментальні компоненти арифметичних логічних одиниць у мікропроцесорах та цифрових процесорах сигналу, повні добавки мають вирішальне значення.ALU обробляє всі арифметичні та логічні операції, при цьому повні доповнення забезпечують обробку даних як швидко, так і точно.

Приклади повного реалізації додавання

Повні доповнення можуть бути побудовані за допомогою різних логічних воріт та конфігурацій.Тут ми досліджуємо чотири різні реалізації, підкреслюючи їх налаштування та оперативні нюанси.

Повний прилад, побудований з XOR, і або воріт

Full Adder Built with XOR, AND, and OR Logic Gates

Малюнок 6: Повний додавець, побудований з XOR, та або логічними воріт

Цей приклад демонструє повний прилад, побудований на дошці, використовуючи дискретні транзистори.Конфігурація включає п’ять логічних воріт: два ворота XOR, дві та ворота та одна або ворота, що вимагає загальної кількості 21 транзисторів.Входи A і B підключені до верхньої дошки зліва, отримуючи запас +5В.Ці входи керуються за допомогою двох перемикачів.Два світлодіоди у верхній лівій частині вказують на стани входів A і B, а два світлодіоди з правого боку відображають виходи.Резистори, що використовуються в ланцюзі, - це 2,2 к Ом.Коли входи A і B увімкнено, а перенесення вимкнено, вихід показує двійкове значення 10, що представляє суму 2 (1 + 1 + 0 = 10).Ворота XOR, побудовані з першими 12 транзисторами, обробляють первинне підсумовування, тоді як нижня половина дошки містить та або або або ворота для операцій перенесення, кольорова проводка підвищує чіткість та усунення несправностей.

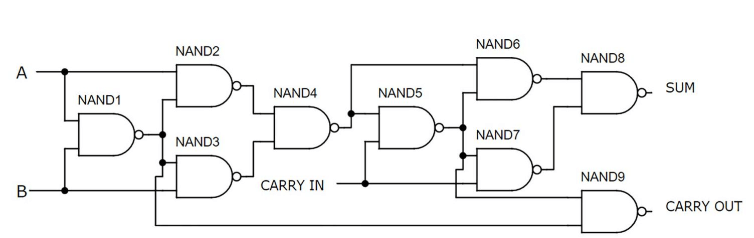
Повна додавання за допомогою воріт NAND

Малюнок 7: Повна додавання за допомогою воріт NAND

Цей повний прилад використовує дев'ять воріт нанд, з кожною воротами, виготовленою з двох транзисторів, загальною частиною 18 транзисторів.Цей метод є одним з найпростіших та найефективніших способів побудови повного додавання за допомогою дискретних компонентів.Всі ворота збираються на верхній половині дошки, а перемикачі займають нижню половину.Функціональність схеми демонструється входами A і B ввімкнено та вимкнено, що призводить до виходу бінарного значення 10, що еквівалентно десятковій 2.

Повна додавання з не воріт

Малюнок 8: Повна додавання з не воріт

Побудований з дев'яти воріт, кожна з яких вимагає двох транзисторів, ця установка також використовує 18 транзисторів.Побудова повного додавання з NOR -Gates пропонує хорошу альтернативу, але передбачає більш складну проводку порівняно з воротом NAND.Кожен транзистор у воріт NOR заземлюється, з колекціонерами, з'єднаними помаранчевими дротяними дротями, щоб забезпечити акуратну та організовану проводку.Ця конфігурація показана з входами A і B, активованою та деактивованою перенесенням, що призводить до виходів, де перенесення активна, і сума вимкнена.

Висновок

Протягом цього дослідження технології ADDER, від основних половин доповнень до складних повних конструкцій, очевидно, що ці компоненти є основоположними для просування цифрової електроніки.Операційні характеристики та приклади впровадження забезпечували універсальність та ефективність добавок у різних обчислювальних умовах.Вивчаючи структуру та функцію добавок, особливо через їхні таблиці правди та характерні рівняння, ми отримуємо цінну інформацію про їхні можливості та обмеження.Ці знання сприяють просуванню більш ефективних та швидших обчислювальних систем.Зрештою, добавки не тільки спрощують складні бінарні розрахунки, але й дають змогу розповсюджувати технологію в таких різноманітних областях, як обробка даних, розподіл пам'яті та обробка цифрових сигналів.У міру розвитку цифрових технологій постійне уточнення та інновації в дизайні Adder надалі залишатимуться наріжним каменем у розробці більш вдосконалених обчислювальних архітектур, гарантуючи, що ці основні компоненти залишаються в основі дизайну та впровадження цифрової системи.

Часті запитання [FAQ]

1. Що таке повна схема додавання?

Повний додавець - це цифровий ланцюг, який додає три бінарні шматочки для отримання суми та виводу перенесення.Він призначений для обробки додавання трьох входів: два значущих бітів та один біт перенесення з попереднього додавання.Це дозволяє використовувати його на послідовних етапах для додавання багатопідрозділених двійкових чисел.

2. Скільки і, чи, xor в повному обсязі?

Типовий повний додавець містить:

Два ворота XOR для генерування суми.

Два та ворота, щоб сприяти розрахунку.

Один або ворота для завершення виводу.

3. Що таке введення перенесення в повному пристрої?

Вхід перенесення (CIN) у повному додавці-це біт перенесення від додавання попередніх нижчих значущих бітів у багатокотковому бінарному додаванні.Це дозволяє повному додавці розглянути цей попередній перенесення при обчисленні поточної суми та нового проведення.

4. Навіщо використовувати повну додавання замість половини додавання?

Повний прилад використовується замість половини додавання, оскільки він може додати три біти (включаючи перенесення з попередніх доповнень), що робить його придатним для ланцюга разом, щоб додати багатокутні номери.Напівплавець може додати лише два біти і не має положення про перенесення, що обмежує його використання найпростішими формами двійкового додавання без послідовного поширення перенесення.

Про нас

ALLELCO LIMITED

Allelco-всесвітньо відомий єдиний зупинка Дистриб'ютор послуг закупівель гібридних електронних компонентів, зобов’язаний надавати комплексні послуги закупівель та ланцюгів поставок для глобальних електронних виробничих та розповсюджувальних галузей, включаючи глобальні 500 фабрик OEM та незалежні брокери.
Дізнайтеся більше